Tipi di frazioni

Studiamo le frazioni individuando con l'aiuto del foglio elettronico se una frazione è già ridotta ai minimi termini e che tipo di numero razionale genera.

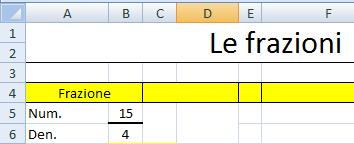
Inseriamo in due celle (ES. B5 e B6) il numeratore e il denominatore di una frazione

Calcoliamo il MCD tra numeratore e denominatore

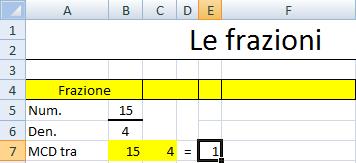
Nella cella E7 è stata inserita la funzione =MCD(B5;B6). Poiché, in questo caso, il MCD =1 si può affermare che la frazione è primitiva. Se il MCD fosse stato diverso da 1 avremmo invece potuto affermare che la frazione era riducibile. Possiamo utilizzare il foglio elettronico con la seguente procedura.

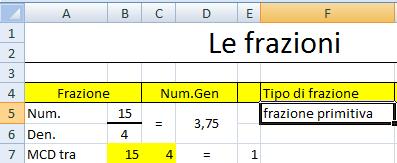
Nella cella F5 è stata inserita la formula: =SE(E7=1;"frazione primitiva";"frazione riducibile!")
Nella cella D5 è stata inserita la formula =SE(NON(VAL.ERRORE(B5/B6));B5/B6;"") che controlla se c'è un errore di qualunque natura (#N/D, #VALORE!, #RIF!, #DIV/0!, #NUM!, #NOME? o #NULLO!): se non ci sono errori calcola il valore del quoziente tra numeratore e denominatore, altrimenti non scrive nulla.

Infine stabiliamo, nel caso di frazione ridotta ai minimi termini, se il numero razionale generato è decimale finito oppure si tratta di un numero periodico

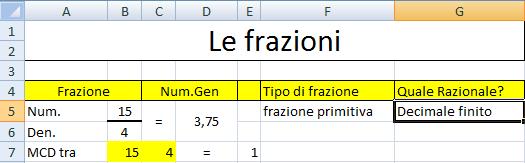
Nella cella G5 è stata inserita la formula
=SE(B6<>"";SE(RESTO(B5;B6)=0;"Numero naturale";SE(F5="frazione riducibile!";"";SE(O(RESTO(B6;2)=0;RESTO(B6;5)=0);"Decimale finito";"Dec periodico"))))

Vediamo di analizzare la precedente formula: nel caso che il denominatore contenga un valore verifica se il resto della divisione è 0 e in questo caso scrive che si tratta di un numero naturale. Nel caso in cui il resto sia diverso da 0, verifica prima che la frazione sia già ridotta ai minimi termini e in questo caso controlla la divisibilità per 2 e per 5 scrivendo che si tratta di un numero decimale finito, altrimenti si tratta di un numero deimale periodico!

Notare l'uso della funzione logica O che restituisce Vero se uno dei suoi argomenti è vero.