Regola di Ruffini

Dato un polinomio P(x), a coefficienti interi, ed il binomio x-k, con k numero
relativo, costruiamo un foglio di lavoro, che assegnato il grado del polinomio P(x), indichi:

• Il numero di coefficienti di P(x)
• Il grado del polinomio quoziente Q(x)
• Il numero dei coefficienti di Q(x)

e, assegnati i coefficienti di P(x), calcolare al variare di k

• i coefficienti di Q(x)
• il resto della divisione

Le formule per l'esecuzione dell'algoritmo sono molto semplici. Dovendo correlare
la prima e la seconda parte occorre rendere assoluti alcuni indirizzi di cella.
Riferendosi al seguente prospetto

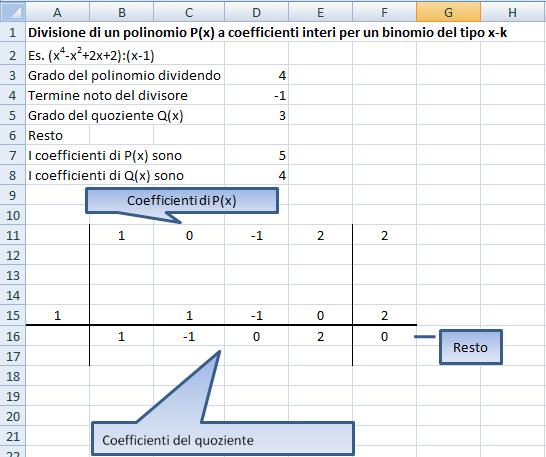
La cella D3 è stata chiamata con il nome N ed in essa è stato inserito il valore 4

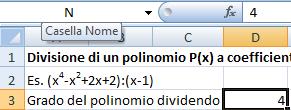
La cella D4 è stata chiamata k ed in essa è stato inserito il
valore -1

Nella cella D5 è stata inserita la formula =N-1
Nella cella D7 è stata inserita la formula =N+1
Nella cella D8 è stata inserita la formula =D5+1
Nella cella A15 è stata inserita la formula =-k

Inseriti i coefficienti del dividendo nelle celle B2:F2, per il calcolo dei
coefficienti del quoziente e del resto si sono inserite le seguenti formule:

in B16 la formula =B11
in C15 la formula =$A$15*B16 copiata quindi nelle celle D15:F15
in C16 la formula =C11-C15 copiata nelle celle D16:F16

Al variare del valore immesso in D4 variano pertanto tutti i coefficienti del
quoziente e il resto.

E' ovvio che tale foglio di lavoro può essere utilizzato per i polinomi
di 4 ° grado. Si può generalizzare il procedimento modificando con
opportune cautele la forma del "castello" in funzione del grado del
polinomio P(x)